Visual Expression Builder component

I’m working on a Java component I’m calling Visual Expression Builder and have done an initial commit to github. The problem I’m trying to address is the limited user interface most applications present for allowing the user to build logical or mathematical expressions.
Now, I understand that most users are flummoxed by high school algebra, but you shouldn’t underestimate the capacity of users to doggedly move bits and pieces around until they work, even if they aren’t entirely sure how something works.
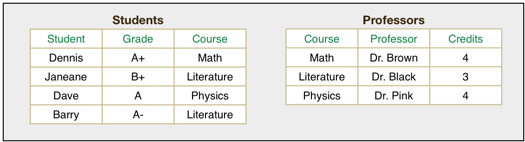
Case study: Address book Smart Groups
Here’s a typical example from Apple’s Address Book application:

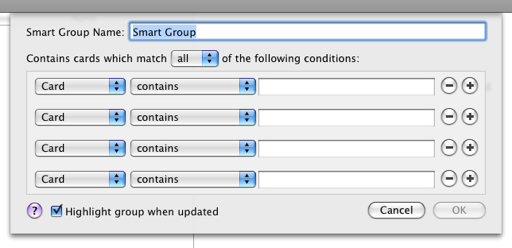
You can use the plus and minus buttons to add constraints and you can choose to match all or just one. It’s tremendously limited; you can’t even say “this and (that or those)”. The problem is that the form metaphor doesn’t scale structure well at all, and it’s a major limitation of all GUIs that are beholden to it.
But this is a good example of the task I’m trying to improve: letting the user build a simple expression, whether it’s criteria for a query or a calculated field or something related.
Case study: OpenOffice.org Function Wizard
Spreadsheets are a more advanced system than what I’m trying to handle. Here’s what OpenOffice’s function wizard looks like:

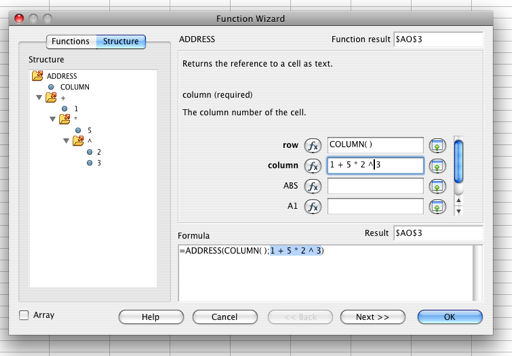
The Function Wizard is more geared towards helping a proficient user (probably an Excel user) migrate to OpenOffice. As such, the user is expected to know some basic concepts of functions, and probably only needs help in a few areas.
The structure diagram doesn’t explain why anything fits where it does and doesn’t allow for manipulation. The right pane is quite helpful in showing the parameters of the function in question. Also, due to its being geared to a proficient user, the function wizard doesn’t provide assistance with arithmetic. I had to guess that ^ was the exponent operator.
One poor assumption the designers make, I think, is that they don’t handle types very well. In the case of OpenOffice, they were building on the design decisions made twenty years ago with Microsoft Excel to use a “typeless” system, and it means that the system knows there’s a type and the user often needs to know there’s a type, but no one wants to admit it.
Case study: OpenOffice.org Query Designer

This is the Query Builder from OpenOffice and shows a very popular way of building an expression. This is optimized towards the common case where users have trouble with complex SQL constructs like grouping. One interesting facet of this is the criterion section. You get conjunction over different fields and disjunction over that, but you really can’t tell just by looking at it. It’s also quite hard to negate a section of the expression; you’d have to know DeMorgan’s law to do it. You also simply have to know that you can enter < 5 in the criteria, which is not a standard mathematical expression at all.
Case study: Circuit layout / network metaphors
On the really high-end there is the CAD software that allows a user to build components. You simply can’t beat actually designing a machine from wires and transistors for flexibility.
Assuming the interface was simplified to only handle basic mathematical expressions, such an interface still runs right into the WYSIWYG Productivity Sinkhole. Modern applications let us lay out documents to pixel perfect precision, and this is often a huge waste of time. Obviously, in some cases it’s worth it to make something look good, but I want users to be able to create an expression without worrying about exactly how it looks.
It’s very hard to allow a person to place components anywhere on the screen and avoid having to tediously move stuff around to no effect.
Proposal: The Puzzle Piece Metaphor
With that in mind, what I’m working on is what I call the puzzle piece metaphor. Nodes, which may be literals, arguments, operators or possibly other elements, are represented as puzzle pieces. The connection is represented as the little nibs that hook puzzle pieces together.
To keep things tidy, we bend the metaphor a bit and allow puzzle pieces to resize dynamically in width, like so:

I didn’t show the nibs in that diagram, but as you can see, the plus operator is wide enough to accommodate all its arguments. Also, the semantics for dragging are fairly straightforward since nibs fit together and pieces resize as necessary. In general, picking up an operator picks up all its precedents. This does mean that you can have separate groups doing separate things, and I may have a receptacle at the bottom of the canvas to set one group to be the official result. Allowing other groups enables the user to build a larger expression from smaller ones, and potentially allows for prefabricated templates. But because pieces fit together and resize automatically and predictably, there’s no messing around with the layout.
Here’s the layout diagram for an operator piece:

It’s pretty easy to generate Bézier paths using Java’s 2D package, and the squiggly puzzle piece lines are going to be fairly subtle so
Although I’m going to experiment with a few different layouts, my intuition is that a simple canvas and toolbox approach is best. An empty component might look like so:

I’ll be posting more on this, hopefully a timetable to get a test applet set up, or you can keep an eye on the github repository.

Identifiers for science should be part of a broader system

There’s an interesting Linked group about identifiers for researchers talking about the issue of unique identifiers for research.
I understand the desire to restrict the problem to a reasonable domain, but some of the suggestions I’ve read seem unrealistic, such as “it’s critical that one researcher only gets one [digital scientist identifier].” (source) That seems like it depends too much on too many people doing the right thing when there’s no reason they should really care to do the right thing.
This really lets the cat out of the bag when it comes to identifying researchers because the whole scientific process expands, but I think most scientists agree that it ought to. A large problem in science is that there’s no serious mechanism for scientists to address falsehoods in the popular media. And while the scientific community may form a consensus on a particular issue, it’s difficult to express this. For example, to express a consensus on evolution a group of scientists launched Project Steve, but that only worked because the consensus was overwhelming.
The larger process begins to make sense if instead of following the publishing model we look at a more general model of interaction made of up smaller actions. Rather than articles as the unit of publishing, you might break it down as far as observations, assertions, arguments, criticisms, etc. Consider a hypothetical chain of events:

• A researcher generates statistical data on cancerous growths.
• The author summarizes the work for a paper.
• The paper is published in a journal.
• An advocacy group cites the paper in a press release.
• The press release is picked up by a journalist.
• A legislator reads the press release.

Now, imagine if a concerned citizen hears about the new law and wants to investigate. There is virtually no way to go back and find the original research and determine if the law in question actually reflects the original science in any way.
To a large extent, the value of research is what people write about it and the actions they take because of that.
After coming back to finish writing this post, I found a very interesting interview on a technology called crossref that does pretty much what I’m asking for. I guess great minds think alike…

Examining a join

Basic concept
The basic concept behind a join is that given two tables you can match rows based on some common attribute.
It’s simple enough in principle:

Join these two tables and you get an extended list of students and their professors:

It’s straightforward enough to think of stepping through each student and looking for the corresponding professor based on the course.
There’s also another way to use a join that might be a little surprising:

This involves joining against an infinite table of areas. It’s really just the times table, only laid out differently than the way it’s traditionally done in elementary school. The idea is that rather than have each row stored on disk, it’s done by lookup data up by passing it to a mathematical function.
Joining against it ought to work like any table. After all, when you look up the living room, you have width = 15 and length = 40, so the area must be 15 ⨉ 40 = 600.
There are problems, though. If it’s going to be just like any other table, you ought to be able to join against any columns. Say you had a table with width and area, it’s easy to see that length = area / width. But some mathematical operations aren’t easily reversed, such as taking a derivative. Some are deliberately difficult, like calculating a hash.
The reason I bring up virtual tables, though, is that it shows how a join can’t be expressed as something as simple as stepping through rows and finding matches. While that seems simple, it’s actually adding complexity.
Cartesian Product
Explaining why takes some doing. We start with the cartesian product.
Let’s go to something basic, the number line:

For now, just consider one point, say x = 4. So we’re just saying one thing about the world: that x is 4. If you add the other points in the line, it means that x = -3 or x = -1 or x = 1, &c.
It’s like a little table:

Let’s add another dimension:

This is another way of saying the same thing. Since we haven’t aid anything about y, it could be anything, hence the infinite vertical lines.
What if we leave x aside and say that y could be 1 or -1?

Right, now let’s ask what happens if (x = -3 or x = -1 or x = 1 or x = 3.5 or x = 5) AND (y = 1 or y = -1)?

It makes sense graphically. After all, I simply superimposed each set of lines and highlighted the points that match. Here’s what it looks like as tables:

Recall that the final table is the same as this:
(x = -3 or x = -1 or x = 1 or x = 3.5 or x = 5) AND (y = 1 or y = -1)
If you don’t remember your boolean algebra, what’s happening is simple distribution:
(a or b or c) and (d or e) = (a and d) or (a and e) or (b and d) or (b and e) or (c and d) or (c and e)
This might look more familiar:
(a + b + c) * (d + e) = a*d + a*e + b*d + b*e + c*d + c*e
Now, I’m not saying they’re the same thing, not by a long shot. For example, you certainly can’t say this:
(5 * 3) + (2 *4) = (5 + 2) * (5 + 4) * (3 + 2) * (3 + 4)
… but you can do that in boolean algebra. The point is that the pattern is the same, and that pattern arises because the cartesian product is essentially the result of asking about this and that.
Why does a join filter out incorrect rows?
The two parts of a join are to perform a cartesian product and then to “filter” the results. Recall the first example:

So, through the process of performing the join we generated every possible combination, and then threw out combinations that didn’t match. That makes sense, but why?
Consider the first row of Students. I’ll claim we’re saying, “Dennis is a student AND the grade is A+ AND the course is math.” So to join Dennis with Literature we’d have to say, “Dennis is a student AND the grade is A+ AND the course is math AND the course is literature AND the professor is Dr. Black AND the Credits are 3.”
By my claim, it’s clear that saying the course is two different things is a logical contradiction. Let’s also recall that the table is really just row OR row OR row. So the rows that are logical contradictions are false values, and when you have false OR true, you can just throw out the false values.
But how can I claim the ANDs I referred to? Consider the table decomposed like so:

These are simple little one column, one row tables. I call them “pairs” because they’re essentially a key-value pair, but they’re basically the smallest unit the relational algebra can address.
Normally, we don’t do cartesian products because the result becomes exponentially large. If you have two tables with 10 rows, the result is 100 rows.
But 1 * 1 * 1 is just 1! So each row is just the cartesian product of its pairs:

And since the whole table can be thought of as the union of its rows. This is a kind of normal form, I call it the “relational sum of products” which should be familiar to anyone whose done circuit design. More interesting is the fact that there actually is a “relational product of sums,” but I’ll get to that later.
Conclusion
The goal with this article was, hopefully, to get into the fine detail of why joins work the way they do. What we’ve covered is the two stages of a join: cartesian product and filtering, and shown the theory of why they work that way, and also, hopefully, made the case that there’s some simple and elegant math behind it. In a future article, I’ll explore the conjoin and disjoin operators and show how various operators are derived from these, and propose a negate operator.

Not another article about the doomed relational model

This one is pretty bad. The author, Mr. Bain, is, according to the bio, the founder of “a company that makes investments in early stage software development.” Well, his article is hype about some new technologies and hype is a necessary reality of life, but if he represents investors he ought to give them better advice than he’s giving in this article.
And from the first line, it doesn’t make sense:

Recently, a lot of new non-relational databases have cropped up both inside and outside the cloud. One key message this sends is, “if you want vast, on-demand scalability, you need a non-relational database”.

After that complete non sequitur:

During this time, several so-called revolutions flared up briefly, all of which were supposed to spell the end of the relational database. All of those revolutions fizzled out, of course, and none even made a dent in the dominance of relational databases.

If he’s just saying that all the silly articles predicting that the relational model was doomed were completely wrong, well, that seems vaguely familiar. But if he’s saying that non-relational technologies were attempted and then abandoned, I’d have to take issue with that. OODBMSs should count as one of the “so-called revolutions” and they’re still around and are, in fact, incorporated in many mainstream SQL DBMSs. Most of the other trendy technologies I can think of, such as XML or some of the data warehousing tech, were never really considered direct competitors to the relational model.
The lesson here is that the marketplace of human ingenuity is always bigger than your imagination and there’s plenty of space for all these various technologies. And, to be clear, I’m not pooh-poohing these technologies, rather, I’d like to follow them more closely because I think they’re extremely interesting. My argument is that they aren’t going to shift relational DBMS technology because they don’t compete with it.
What exactly is it that the relational database dominates, and how does it dominate? The what of the answer isn’t way out there, and it surprises me that a business guy like Mr. Blain missed it.
Here’s the basic business reason for a SQL DBMS: your business has many processes that involve many (metaphorical) moving parts and you need to capture that logic, known as business logic, in a set of rules. You need your data to conform, at all times, to those rules.
This isn’t to say that there isn’t a whole lot of other data that can’t be stored in other ways or even must be stored in other ways, but here are a few of the things that businesses have to worry about:

• Tracking employees.
• Paying taxes.
• Government regulations.
• Tracking customers.
• Tracking shipments.
• Managing vendors.

This stuff goes back to before the Roman Empire, and, if anything, it’s only going to get more regulated and more complex, which means the need to track business logic, and thus the case for the relational DBMS, will only grow.
The second half of the answer, the how, is that the relational model is well defined. DBMSs using SQL (which is pretty much all of them) don’t use the relational model but what is often referred to as the SQL model. The differences between the relational model and the SQL model are a little arcane (and I’ll probably touch on them in this blog) but they are significant enough that it’s simply wrong to conflate the two.
Many of the competitors to the relational model, such as the old Pick systems (still around, incidentally) used a model that was not well defined. So what’s wrong with loosely defined systems? There are a few, but I’d argue the complete and total lack of interoperability is the problem. At first blush XML refutes this, but really, it proves it.
What did we have pre-XML? A complete mess of binary formats, and the n-squared problem of writing translators for all of them. Did you ever try these translators? Even simply opening a Word document in a later version tends to destroy the underlying data.
Along comes the web and the successful tag structure of HTML is generalized to arbitrary data. LISP advocates complain that it’s just symbolic expressions with angle brackets.
So now we have a post-XML world. DOC has become DOCX and what’s changed? Well, loading and saving documents is somewhat more robust because some of the logic has been offloaded to reusable libraries. And now you can use XSLT to transform documents.
But the original problem remains: you have a whole mess of incompatible file formats and n-squared translators that don’t actually work.
The various key-value stores are very new, and it remains to be seen how well they will work together, but I haven’t seen any evidence that they even attempt to address the issue.
(Updates: 4 Mar: formatting.)